函数上的最大曲率点
·
Package Build
在一些数据分析任务中,我们有时需要将数据拟合成曲线,并试图确定一个拐点来解释性质变化。那么,如何才能精确地找到这个拐点?
比如:
这里介绍R语言soilphysics包中的maxcurv()函数,来帮我们计算出函数曲线上的最大曲率点。
它的一般用法:
maxcurv(x.range, fun, method = c("fd", "pd"), graph = TRUE)
# x.range: x 范围,一个包含两个元素的向量,表示曲线的取值范围。
# fun: 要计算曲率的函数,必须是一个可调用的 R 函数。
# method: 计算曲率的方法,可以是 "fd"(有限差分法)或 "pd"(抛物线拟合法)。
# graph: 是否显示计算过程的图形,默认为 TRUE。
返回值是一个列表,包含以下元素:
# x0: 最大曲率点的 x 坐标。
# y0: 最大曲率点的 y 坐标。
# curvature: 最大曲率点处的曲率值
原理:
- 对于给定的函数,首先在指定范围内生成足够密集的点。
- 根据指定的方法(有限差分法或抛物线拟合法),计算每个点处的曲率值。
- 找到曲率值最大的点,即为最大曲率点。
- 返回最大曲率点的坐标和曲率值。
示例1:
x_min = 1
x_max = 20
mc <-
\(f) {
soilphysics::maxcurv(
x.range = c(x_min, x_max),
fun = f,
method = "pd",
graph = FALSE
)
}
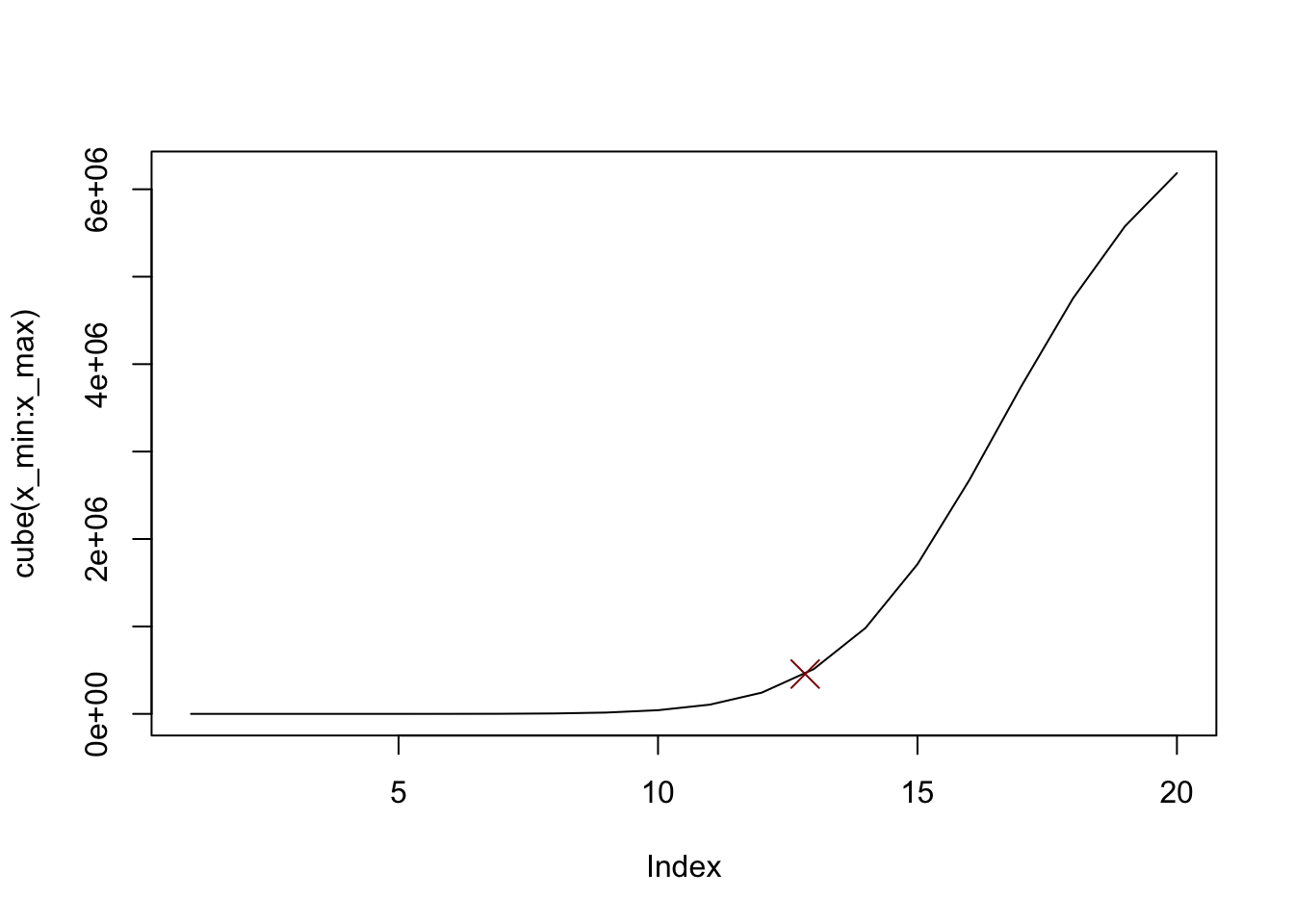
# cubic
cube <- \(x) 7424243 + (1.679594 - 7424243) / (1 + (x / 16.96819)^9.773759)
r <- mc(cube)
plot(cube(x_min:x_max), type = "l")
points(r$x0, r$y0, col = "darkred", pch = 4, cex = 2)
示例2:
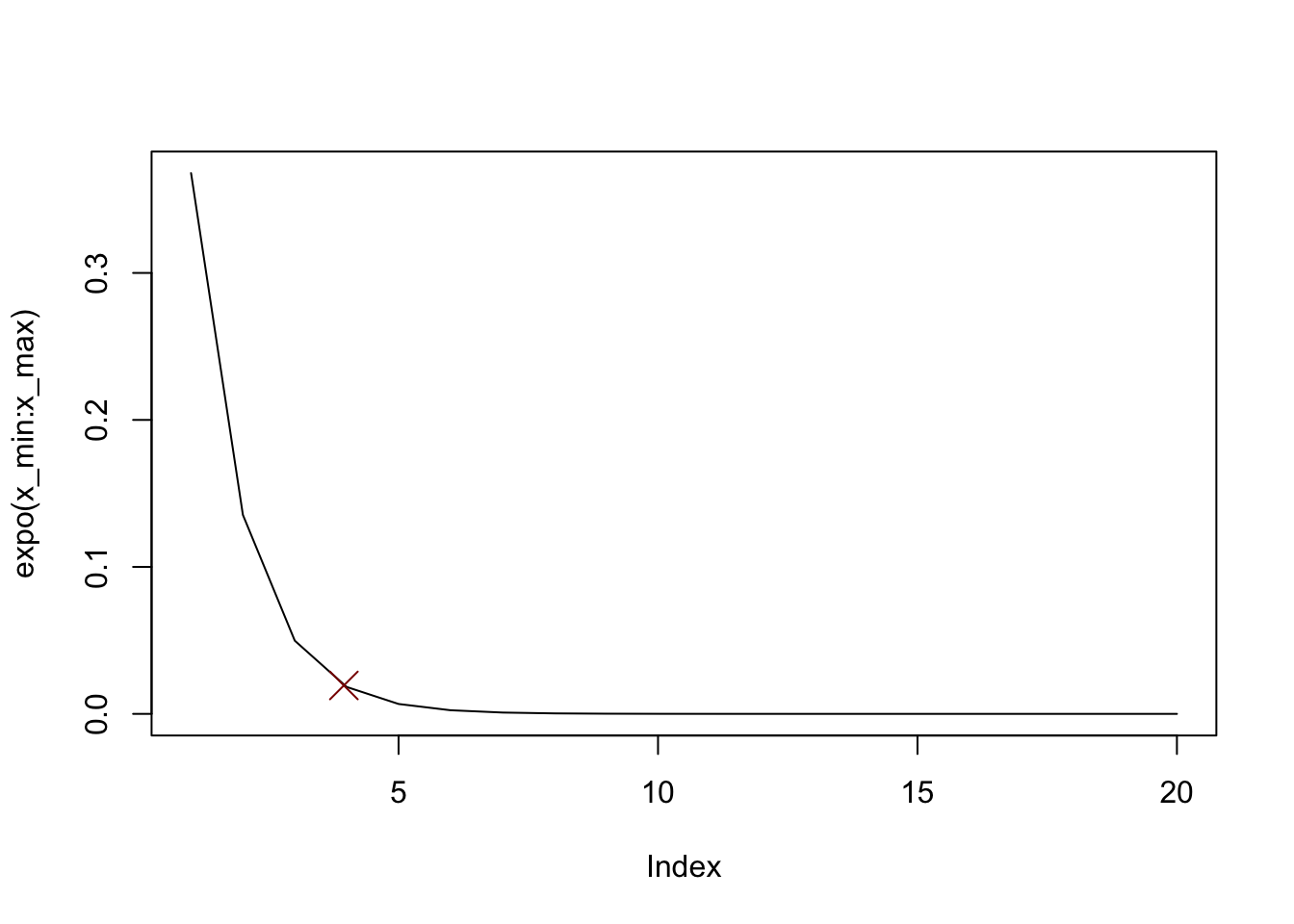
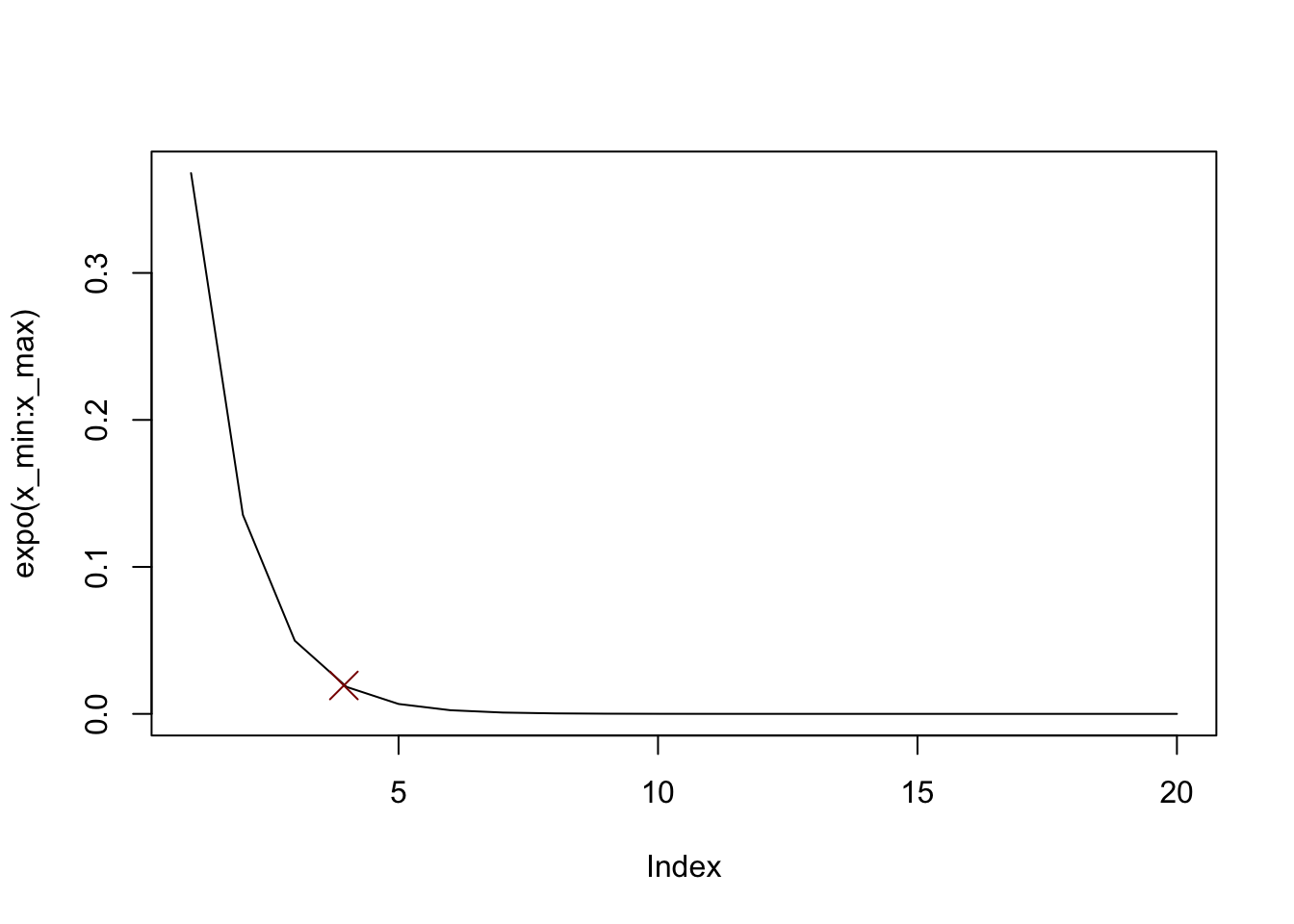
# exponential
expo <- \(x) exp(-x)
r <- mc(expo)
plot(expo(x_min:x_max), type = "l")
points(r$x0, r$y0, col = "darkred", pch = 4, cex = 2)