KL散度模拟
·
Xiebro
从采样角度出发对KL散度进行直观解释,即:KL散度描述了我们用分布Q来估计数据的真实分布P的信息(编码)损失。
附:一篇关于Kullback-Leibler Divergence 基本介绍的blog
验证问题
假如真实样本P已知,Q是对P的随机采样样本,那么Q相对于P的信息损失是否与采样样本量呈线性关系?
换句话讲,假如Q的样本量与P相等,那么Q可以100%程度表述P的信息,假如Q的样本量是P的10%呢?此时是否会相较于前者损失90%的信息?即KL散度与样本量是否是线性的关系?
模拟验证
library(tidyverse)
library(furrr)
library(hrbrthemes)
theme_set(theme_ipsum(base_family = "Kai", base_size = 8))
plan(multisession, workers = 10)
set.seed(42)
# 模拟总体样本P
P <- rbinom(10000, 1, 0.1)
cat(paste0("总体样本P的样本量:", length(P),", 均值:", mean(P)))
## 总体样本P的样本量:10000, 均值:0.1031
# bootstrap估计P的均值分布
trials <- 10000
P_norm <-
1 : trials |>
future_map_dbl(~ {
P |>
sample(replace = TRUE) |>
mean()
})
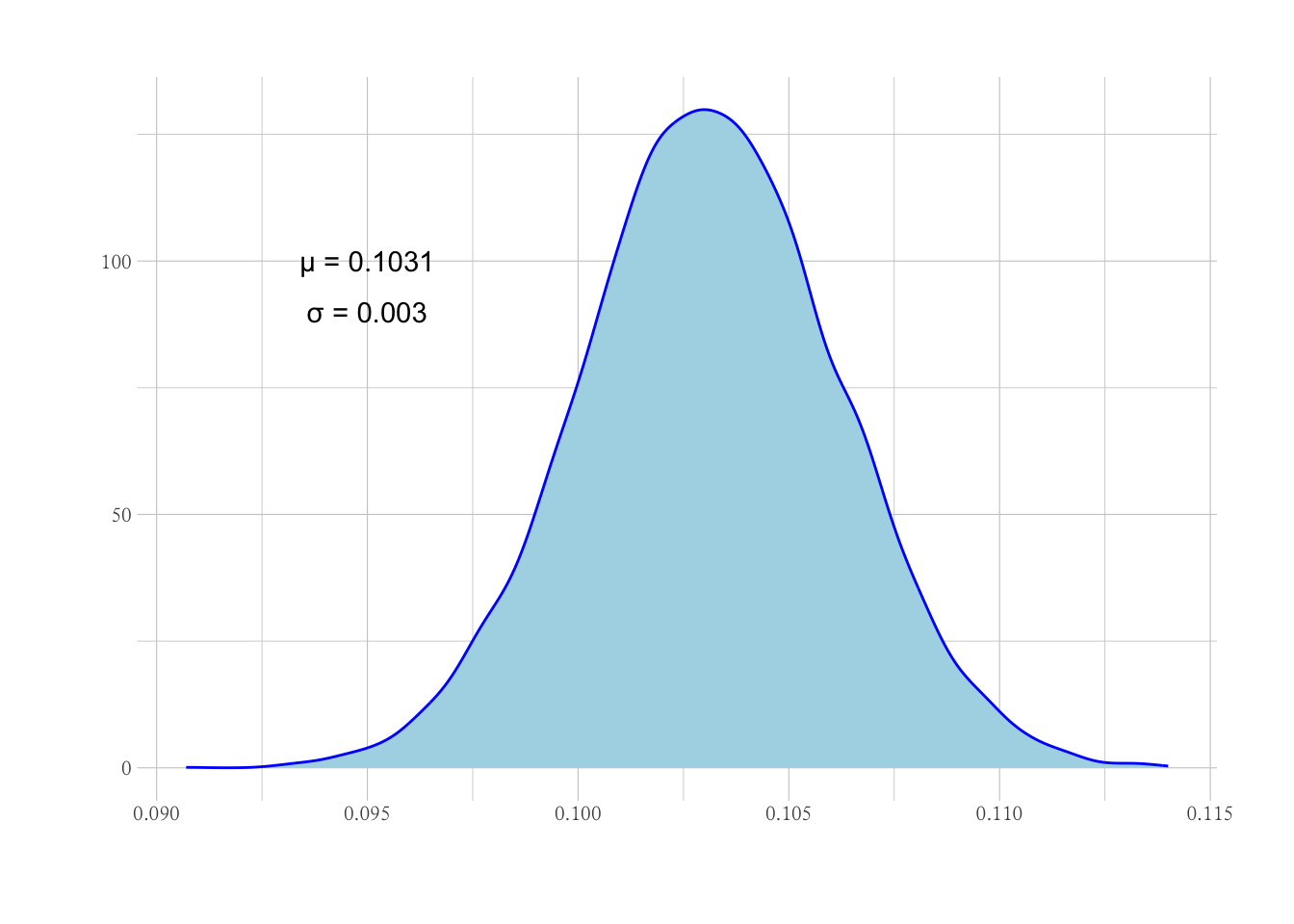
cat(paste0("P的均值分布参数: μ = ", mean(P_norm), ", σ = ", sd(P_norm)))
## P的均值分布参数: μ = 0.10312768, σ = 0.00304222078888647
NULL |>
ggplot(aes(P_norm)) +
geom_density(col = "blue", fill = "lightblue") +
geom_text(aes(x = 0.095, y = 100, label = paste0("μ = ", round(mean(P_norm), 4)))) +
geom_text(aes(x = 0.095, y = 90, label = paste0("σ = ", round(sd(P_norm), 4)))) +
labs(x = "", y = "")
# 对P进行采样生成Q,Q样本量为P的n%时的均值分布
nsize_pct <- 0.10
Q_norm <-
1 : trials |>
future_map_dbl(~ {
P |>
sample(size = nsize_pct * length(P),
replace = TRUE) |>
mean()
})
# 计算Q与总体P的KL散度
kl <- function(mu1, sigma1, mu2, sigma2) {
re <- log(sigma2 / sigma1) + (sigma1^2 + (mu1 - mu2)^2) / (2 * sigma2^2) - 0.5
return(re)
}
kl_val <- kl(mean(P_norm), sd(P_norm), mean(Q_norm), sd(Q_norm))
df <-
data.frame(
val = c(P_norm, Q_norm),
grp = rep(c("P_norm", "Q_nrom"), times = c(length(P_norm), length(Q_norm))))
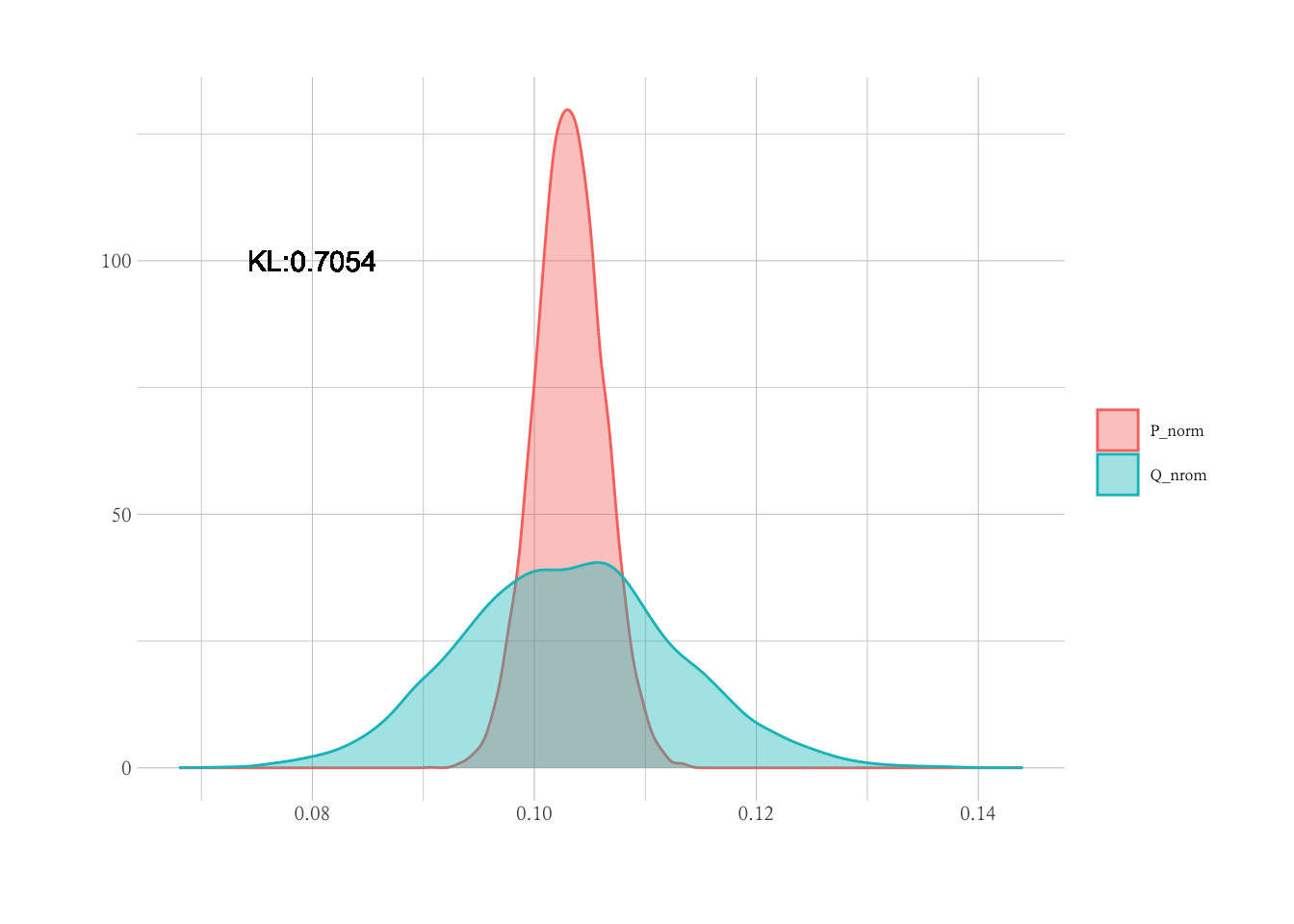
df |>
ggplot(aes(x = val, col = grp, fill = grp)) +
geom_density(alpha = 0.4) +
geom_text(x = 0.08, y = 100, label = paste0("KL:", round(kl_val, 4)), col = "black") +
labs(x = "",
y = "",
col = "",
fill = "")
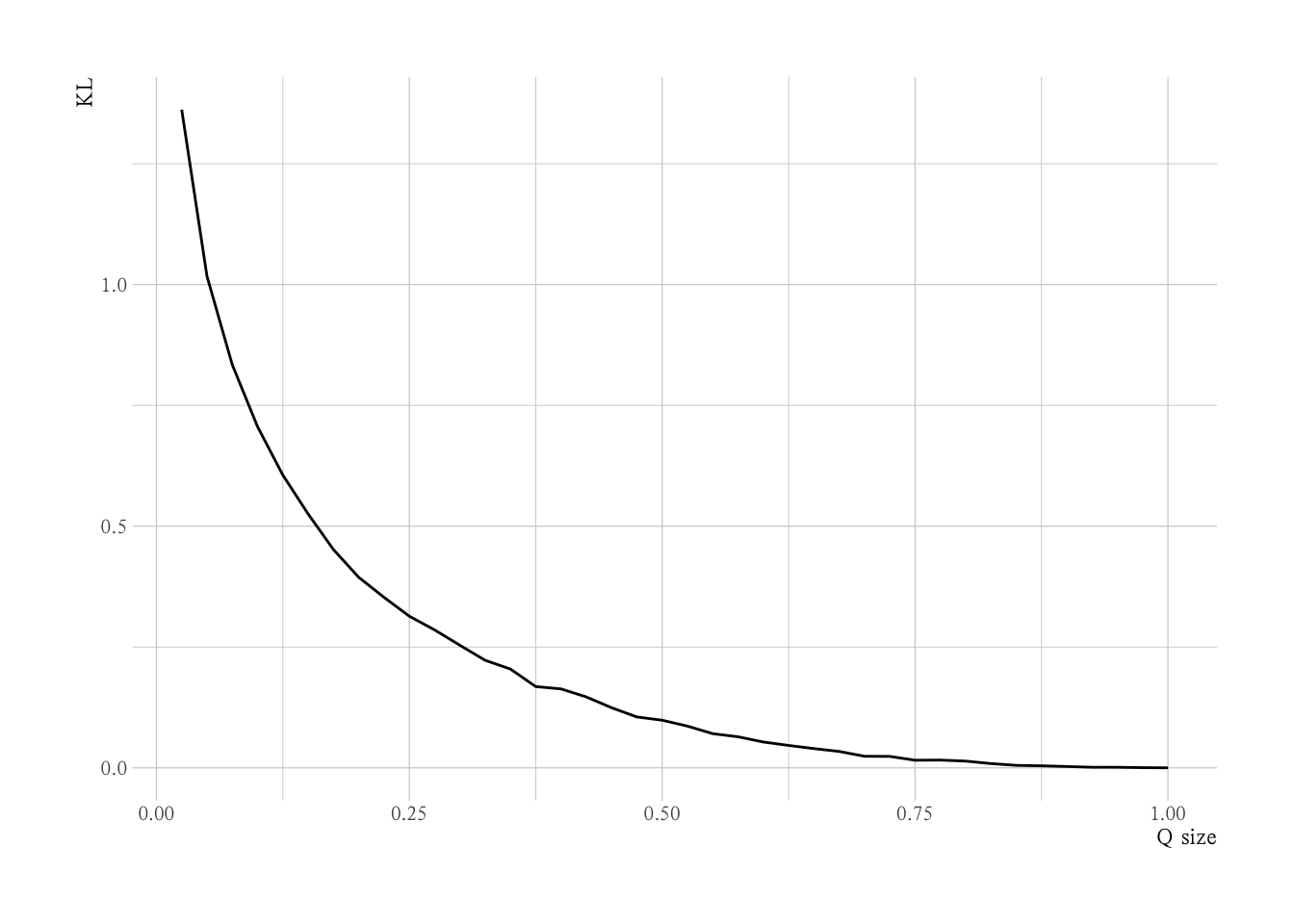
# KL散度与采样样本量的关系
run_simulate <- function(nsize_pct, P, P_norm, trials = 1e4){
Q_norm <-
1: trials |>
future_map_dbl(~ {
P |>
sample(size = nsize_pct * length(P), replace = TRUE) |>
mean()
})
kl(mean(P_norm), sd(P_norm), mean(Q_norm), sd(Q_norm))
}
nsize_pct <- seq(0.025, 1, by = 0.025)
re <-
nsize_pct |>
future_map_dbl(~{
run_simulate(.x, P, P_norm)
})
NULL |>
ggplot(aes(x = nsize_pct, y = re)) +
geom_line() +
labs(x = "Q size",
y = "KL")