囚犯盒子问题
·
Xiebro
囚犯盒子问题(Prisoners and Boxes Problem)是一个经典的数学与概率问题,通常涉及策略设计和成功概率的计算,问题设定如下:
问题描述
假设有100名囚犯,每人都带有一个独特编号(1到100)。
囚犯们被带到一个房间,房间里有100个密封的盒子,每个盒子中都有一张纸条,上面写着一个囚犯的编号。
这些编号被随机放置在盒子里,也就是说,盒子中编号与囚犯编号的顺序是随机的。
每个囚犯按顺序进入房间,在最多只能打开50个盒子的前提下,找到写有自己编号的纸条。
每个囚犯离开房间后,盒子的状态会恢复原样,其他囚犯不会知道之前的情况。
囚犯们事先可以商量策略,但进入房间后不能交流或做任何标记。
如果所有囚犯都能在50次尝试内找到自己的编号,囚犯们将获释;否则,如果有1个囚犯没有找到自己的编号,所有囚犯都会被处决。
问题关键点
- 100个囚犯(编号从1~100)
- 随机将囚犯编号放入房间里的100个盒子
- 每次只允许1个囚犯进入房间,可以检查50个盒子
- 囚犯离开时必须恢复原样,且不能与其他人交流
- 如果100个囚犯都找到了自己的编号,则全部获释,反之,则全部处决
所以,每个囚犯在没有策略的情况下成功找到自己编号的概率是50%,而所有囚犯都成功的概率:
$$ P = \left(\frac{1}{2} \times \frac{1}{2} \times \dots \right) = \left(\frac{1}{2}\right)^{100} $$
计算结果为:0.0000000000000000000000000000007888609,几乎为零。
策略
有一种基于“循环链”概念的策略可以将成功概率提高到30%以上:
- 每个囚犯开始时先打开与自己编号相同的盒子。例如,囚犯1会先打开1号盒子,囚犯2会先打开2号盒子,以此类推。
- 如果盒子里的纸条不是自己的编号,囚犯将根据纸条上编号所指的盒子继续打开(例如,囚犯1打开1号盒子发现纸条上写的是57,那么他接着去打开57号盒子),依次重复直到找到自己的编号或达到50次为止。
- 这种策略构造了一个循环:编号会形成若干个闭环链条,相同链条上的囚犯有着相同的结果,如果最长的链条长度<=50,那么所有链条上的囚犯都会成功,如果最长的链条长度>50,那么该链条上的所有囚犯都失败。
所以,基于这个策略,也可以将问题转换为:
100个盒子随机组成若干链条,最大的链条长度不超过50的概率是多少?
模拟
library(tidyverse)
set.seed(42)
trials <- 10000 # 模拟实验次数
N <- 100 # 每次实验的囚犯或盒子数量
方法1:
模拟每个囚犯按照策略寻找,直到找到自己编号或检查50个盒子后停止
# 单个囚犯的检查结果
check_box_chain <- function(pn, box){
counter <- 0 # 初始化:已查看盒子数
box_n <- pn # 初始化:查看的盒子编号
num <- -1 # 初始化:打开盒子后的数字
while(counter <= 0.5 * N & num != pn){
num <- box[[box_n]]
box_n <- num
counter <- counter + 1
}
return(num == pn)
}
# 单次实验的最终结果
perform_once <- function(){
box <- sample(1 : N, size = N, replace = FALSE)
res <-
1 : N %>%
map_vec(~{
check_box_chain(pn = .x, box = box)
})
return(!any(res == FALSE)) # T-成功,F-失败
}
# 执行
result <-
1 : trials %>%
map_vec(~ perform_once())
paste0("经过", trials, "次模拟得出,囚犯的成功概率为:", mean(result) * 100, "%" )
## [1] "经过10000次模拟得出,囚犯的成功概率为:32.92%"
方法2:
计算随机组成的最大闭环长度,不大于50的概率
# 单个盒子最大链条长度计算
length_box_chain <- function(box){
res <-
1 : N %>%
map_vec(~{
num <- box[[.x]]
counter <- 1
while(num != .x){
num <- box[[num]]
counter <- counter + 1
}
counter
})
return(max(res)) # 返回最大链条长度
}
# 执行
result <-
1 : trials %>%
map_vec(~{
box <- sample(1 : N, size = N, replace = FALSE)
length_box_chain(box)
}) %>%
as.data.frame() %>%
setNames("chain_length") %>%
mutate(
fill_type = ifelse(chain_length > 0.5 * N, "Fail", "Success"),
boole_type = ifelse(chain_length > 0.5 * N, FALSE, TRUE)
)
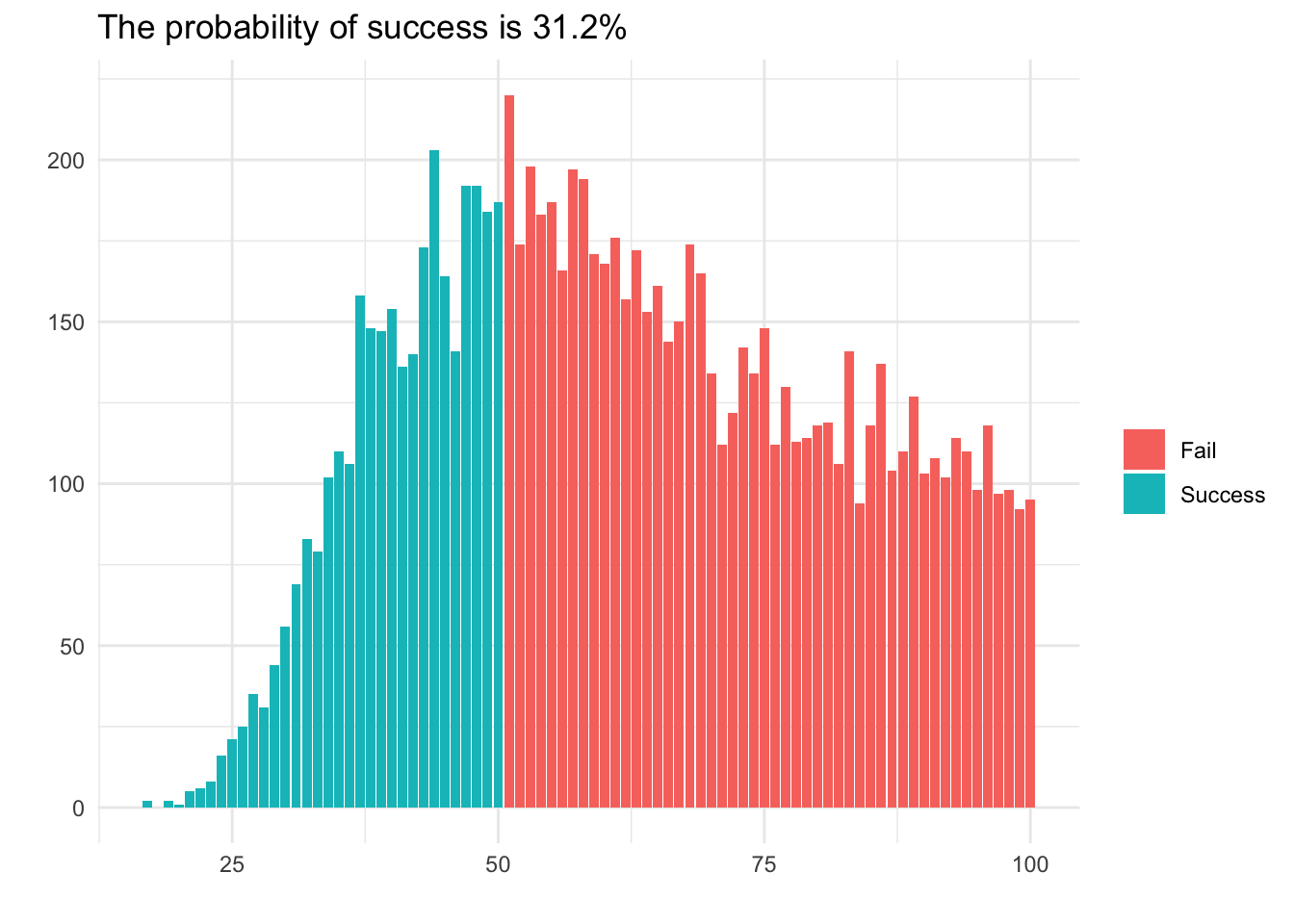
result %>%
ggplot(aes(x = chain_length)) +
geom_bar(aes(fill = fill_type)) +
theme_minimal() +
labs(
x = "",
y = "",
fill = "",
title = paste0("The probability of success is ", mean(result$boole_type) * 100, "%")
)