猜猜篮子里有多少苹果
·
Xiebro
问题场景
- 在一个桶里,有同等数量的红苹果与青苹果,但你并不知道具体数量。
- 你随机抽取了 19 个,发现拿了红苹果 8 个,青苹果 11 个。
- 针对刚才桶里苹果的总数量(红与青之和),最好的猜测是多少?
- 注:为了卫生起见,拿出任何一个苹果后就不准再放回桶里。
这是一个参数估计的概率问题,具体来说是通过已知的样本信息来估计总体参数的值。
在这个情景中,我们知道从一个桶中抽取了19个苹果,其中8个是红色的,11个是青色的。我们并不知道桶中到底有多少个苹果,但我们想要估计红色和青色苹果的总数量。
因此,我们需要考虑在不同假设下(桶中红色苹果的数量),得到观察样本的概率。然后,我们找到使得这一概率最大化的假设,即我们的最佳估计。
换句话说就是:当篮子里有多少个苹果时,你有最大的概率会抽到8红11青。
所以我们可以通过蒙特卡洛模拟计算:
- 当篮子里有11个红(或青)苹果时(即总共22个),抽到8红11青的概率是p11
- 当篮子里有12个红(或青)苹果时(即总共24个),抽到8红11青的概率是p12
- ……
- 当篮子里有n个红(或青)苹果时(即总共2n个),抽到8红11青的概率是pn
Monte-Carlo Simulation
library(purrr)
# 场景复刻
nn_size = 19
nn_red = 8
nn_green = 11
# 生成一个装有2n个苹果的篮子(0:红, 1:青)
generate_bin <- function(n) {
rep.int(c(0L, 1L), n)
}
# 实验设计
run_experiment <- function(n, trials = 10e3) {
if (n < max(nn_red, nn_green)) return(0L)
reps <- replicate(
trials,
n |>
# 生成篮子
generate_bin() |>
# 随机不放回抽样
sample(size = nn_size, replace = FALSE) |>
# 判断结果是否符合预期
sum() == nn_green
)
# 预期结果出现的概率=预期结果出现的次数/总抽样次数
sum(reps) / trials
}
# 实验进行
set.seed(1234)
res <- purrr::map_dbl(2:50, run_experiment)
# 出现最大概率时所对应的红(青)苹果数量
N <- which(res == max(res))
可视化
library(ggplot2)
NULL |>
ggplot(aes(x = 1:length(res), y = res))+
geom_step()+
geom_vline(xintercept = N,
col = "salmon",
lty = 4)+
geom_text(aes(x = N + 2,
y = 0.025,
col = "red",
label = N))+
guides(col = "none")
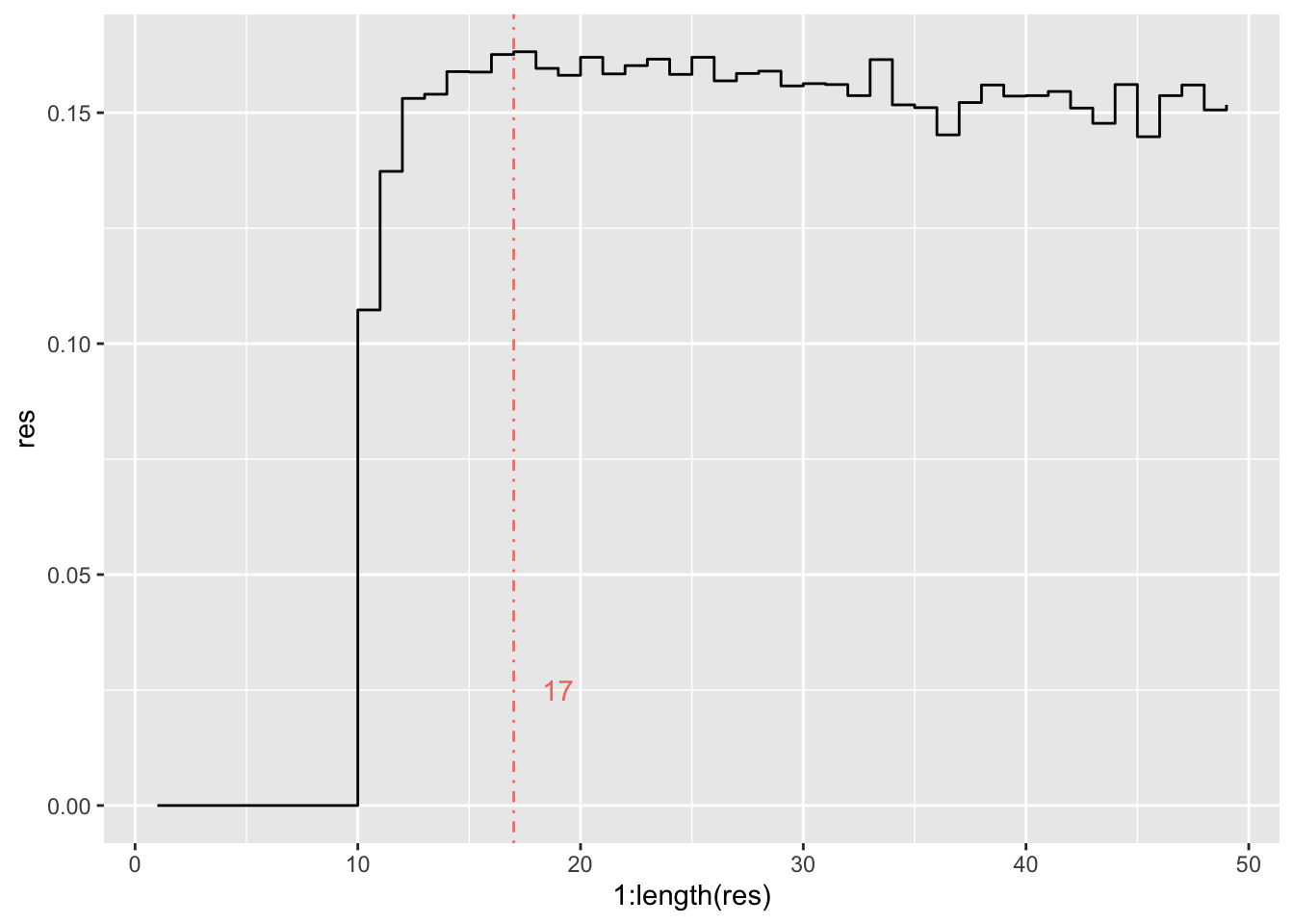
所以,最好的猜测是:总共34个苹果。