Home

AB实验方差缩减技术---CUPED

· Package Build

CUPED（Controlled-experiment Using Pre-Experiment Data） 是一种在 A/B 实验 中利用 实验前数据 来 降低指标方差、提高统计功效 的方法。它本质上是一次 协变量调整（回归去噪）。

一、核心原理

  1. 问题背景
    在 A/B 实验中，核心指标 𝑌（如转化率、完课用时）通常波动较大，需要更长时间或更大样本量才能检验出差异。
  2. 关键思想
    如果存在一个实验前的历史指标 𝑋 且它与实验期指标 𝑌 高度相关，那么：
  • X 中包含了用户“先天差异”（活跃度、消费能力、学习能力等）
  • 这些差异会无差别地混入实验期指标 𝑌 的噪声中

CUPED 的做法是： 把 𝑌 中可由 𝑋 解释的那一部分“减掉”，只保留更“干净”的随机波动。

二、场景示例

评估“新课程讲解方式”是否能缩短完课时间

  • 实验目标（Y）：用户在实验期的「单元首次完课用时」
  • 实验前指标（X）：同一用户在实验前的「历史平均完课用时」

示例设定：

  • 每个用户有一个先天能力（不可观测）
  • 实验前指标 X（历史完课用时）≈ 能力 + 噪声
  • 实验期指标 Y（实验期完课用时）≈ 能力 + 实验效应 + 噪声
  • 实验组相对对照组 真实提升 = -2 分钟

对比：原始指标 Y vs. CUPED 调整后指标 Y_cuped

library(dplyr)
library(tidyr)
library(ggplot2)
library(showtext)
showtext::showtext_auto()
set.seed(123)
# -----------------------------
# 1. 构造模拟数据
# -----------------------------
n <- 1000

df <- tibble(
  user_id = 1:n,
  group = sample(c("control", "treat"), n, replace = TRUE)
)

# 用户先天能力（不可观测）
ability <- rnorm(n, mean = 50, sd = 10)

# 实验前指标 X
df$X <- ability + rnorm(n, sd = 5)

# 实验真实效果（treat 缩短 1）
treatment_effect <- ifelse(df$group == "treat", -2, 0)

# 实验期指标 Y
df$Y <- ability + treatment_effect + rnorm(n, sd = 10)

# -----------------------------
# 2. CUPED 调整
# -----------------------------
theta <- cov(df$Y, df$X) / var(df$X)

# 或者使用线性回归：
# model <- lm(Y ~ X, data = df)
# theta <- coef(model)["X"]

df <- df |>
  mutate(
    Y_cuped = Y - theta * (X - mean(X))
  )

# -----------------------------
# 3.1 数值结果对比（打印）
# -----------------------------
summary_tbl <- df |>
  group_by(group) |>
  summarise(
    mean_Y = mean(Y),
    var_Y  = var(Y),
    mean_Y_cuped = mean(Y_cuped),
    var_Y_cuped  = var(Y_cuped),
    .groups = "drop"
  ) |>
    mutate(across(where(is.numeric), round, 2))

knitr::kable(summary_tbl, caption = "A/B 组指标对比（原始 vs CUPED）", format = "html")
Table 1: A/B 组指标对比（原始 vs CUPED）
group mean_Y var_Y mean_Y_cuped var_Y_cuped
control 49.88 205.86 49.88 116.38
treat 48.38 187.12 48.38 114.74 
# -----------------------------
# 3.2 显著性检验（Raw vs CUPED）
# -----------------------------

# 原始指标 t 检验
t_raw <- t.test(
  Y ~ group,
  data = df
)

# CUPED 指标 t 检验
t_cuped <- t.test(
  Y_cuped ~ group,
  data = df
)

pval_tbl <- tibble(
  metric = c("Raw", "CUPED"),
  mean_diff = c(
    diff(t_raw$estimate),
    diff(t_cuped$estimate)
  ),
  p_value = c(
    t_raw$p.value,
    t_cuped$p.value
  )
) |>
  mutate(
    mean_diff = round(mean_diff, 3),
    p_value = signif(p_value, 3)
  )

knitr::kable(
  pval_tbl,
  caption = "显著性检验结果对比（Raw vs CUPED）",
  format = "html"
)
Table 1: 显著性检验结果对比（Raw vs CUPED）
metric mean_diff p_value
Raw -1.501 0.0908
CUPED -1.506 0.0270 
# -----------------------------
# 4. 可视化 ：整体分布对比
# -----------------------------
df |>
  select(group, Y, Y_cuped) |>
  pivot_longer(
    cols = c(Y, Y_cuped),
    names_to = "metric",
    values_to = "value"
  ) |>
  mutate(
    metric = factor(
      metric,
      levels = c("Y", "Y_cuped"),
      labels = c("Raw", "CUPED")
    )
  ) |>
  ggplot(aes(x = group, y = value, fill = group)) +
  geom_boxplot(
    width = 0.6,
    outlier.alpha = 0.2
  ) +
  facet_wrap(~ metric) +
  labs(
    title = "原始指标 vs CUPED 调整后指标分布对比",
    x = "",
    y = "完课用时"
  ) +
  theme_minimal()

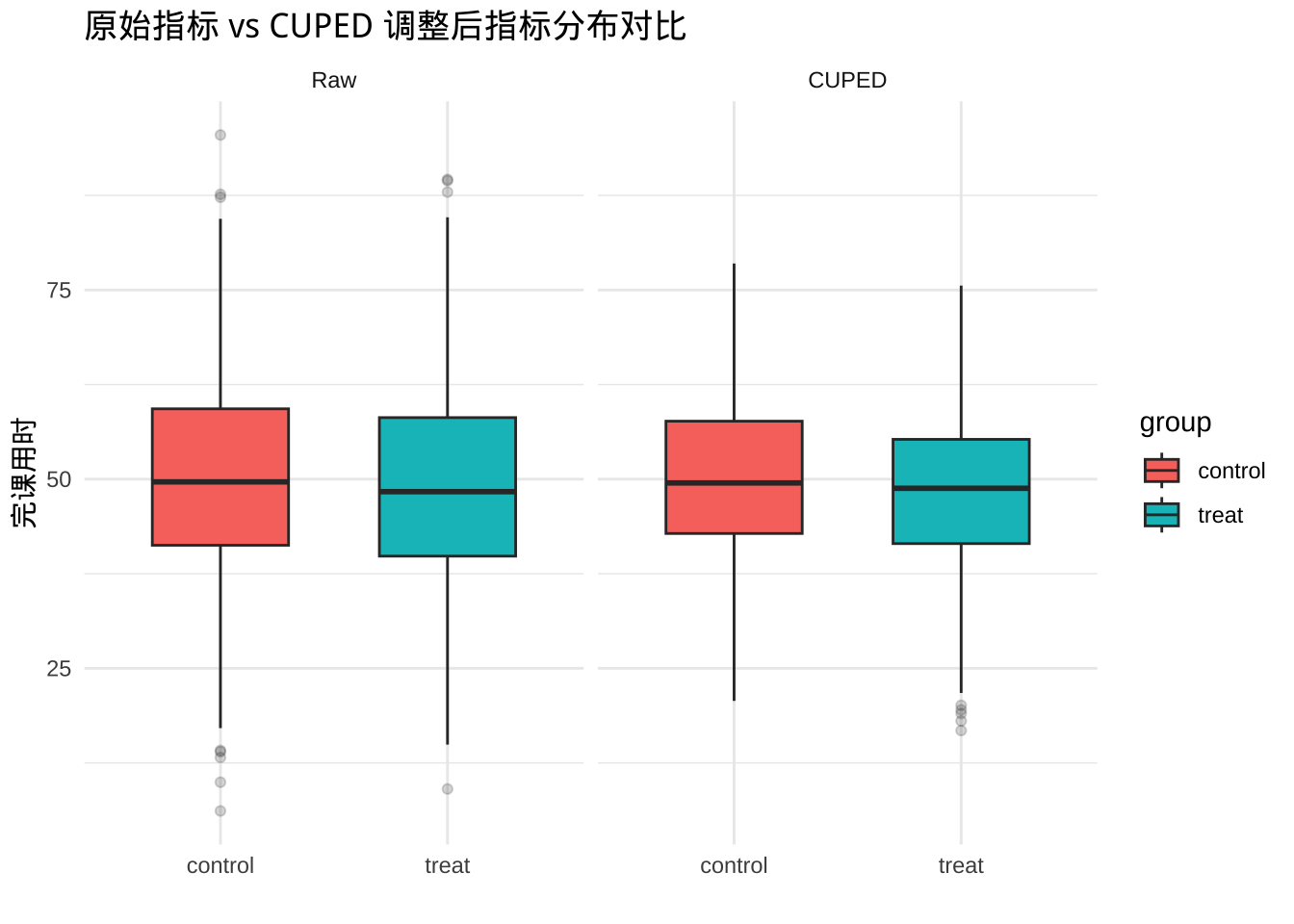
CUPED 在不改变组间期望差异的前提下，通过去除与实验无关的个体差异，显著降低组内方差，从而提升显著性检验的效率。

“不动信号，只降噪声！”

三、注意以下情况不可用

  1. 非随机分组
  2. 𝑋不是实验前指标，或被实验机制影响（θ是用实验前的𝑋和实验期的𝑌做回归）
  3. 幸存者偏差，只有完成实验期的人才有𝑋
  4. 在组内分别估计 θ（正确做法是全样本估计）
  5. 存在极端值时（建议先对 𝑋 和 𝑌 做变换，如 log）
  6. 在指标波动本身小或历史指标相关性低的情况下，方差收益可能不明显