P-Value的可靠性模拟
·
Xiebro
要验证的问题:
在不同的实验条件下,我们使用P值衡量两组样本的差异显著性,是否是可靠的? 举个例子,假如以下都是正态分布的样本:
- 当样本量及参数(μ、σ)不变,仅改变随机种子,多次得到的P值结果是否是稳定的?
- 当随机种子和样本参数(μ、σ)均不变,仅改变样本量,所得到P值结果是否是稳定的?
- …
当改变了样本的样本量、参数、以及随机种子时,分别对P值的影响如何?
进行模拟
library(tidyverse)
library(infer)
library(furrr)
library(hrbrthemes)
theme_set(theme_ipsum_rc())
plan(multisession, workers = 10)
# 模拟两个分布并进行置换检验,得到均值差异和P值
run_simulate <- function(nsize, mudiff, sigma, seed){
set.seed(seed)
base_mean <- 0.10
grp_A <- rnorm(nsize, mean = base_mean, sd = sigma)
grp_B <- rnorm(nsize, mean = base_mean + mudiff, sd = sigma)
obs <- mean(grp_A) - mean(grp_B)
dat <-
tibble(grp_A, grp_B) |>
mutate(id = ids::random_id(n = n(), bytes = 2)) |>
pivot_longer(cols = -id,
names_to = "grp",
values_to = "score")
df <-
dat |>
specify(score ~ grp) |>
hypothesise(null = "independence") |>
generate(reps = 1000, type = "permute") |>
calculate(stat = "diff in means", order = c("grp_A", "grp_B"))
re <- list(
diff_in_means = mean(df$stat),
p_value = get_p_value(df, obs_stat = obs, direction = "left")[["p_value"]]
)
return(re)
}
先模拟两次
run_simulate(nsize = 30, mudiff = 0.01, sigma = 0.03, seed = 4)
## $diff_in_means
## [1] 4.721894e-05
##
## $p_value
## [1] 0.802
run_simulate(nsize = 30, mudiff = 0.01, sigma = 0.03, seed = 123)
## $diff_in_means
## [1] -0.0005003721
##
## $p_value
## [1] 0.008
从上述两次模拟结果中可见,在固定的示例参数下仅仅改变了随机种子,所得到的P值是相当不稳定的。
多次模拟
# 多次模拟分布的参数
pars <- expand_grid(
nsize = seq(10, 100, 15),
mudiff = seq(0.01, 0.05, 0.01),
sigma = seq(0.01, 0.05, 0.01),
seed = sample(1:9999, 10, replace = FALSE)
)
res <-
future_pmap(pars, ~ {
run_simulate(nsize = ..1, mudiff = ..2, sigma = ..3, seed = ..4)
})
df <-
res |>
bind_rows() |>
bind_cols(pars)
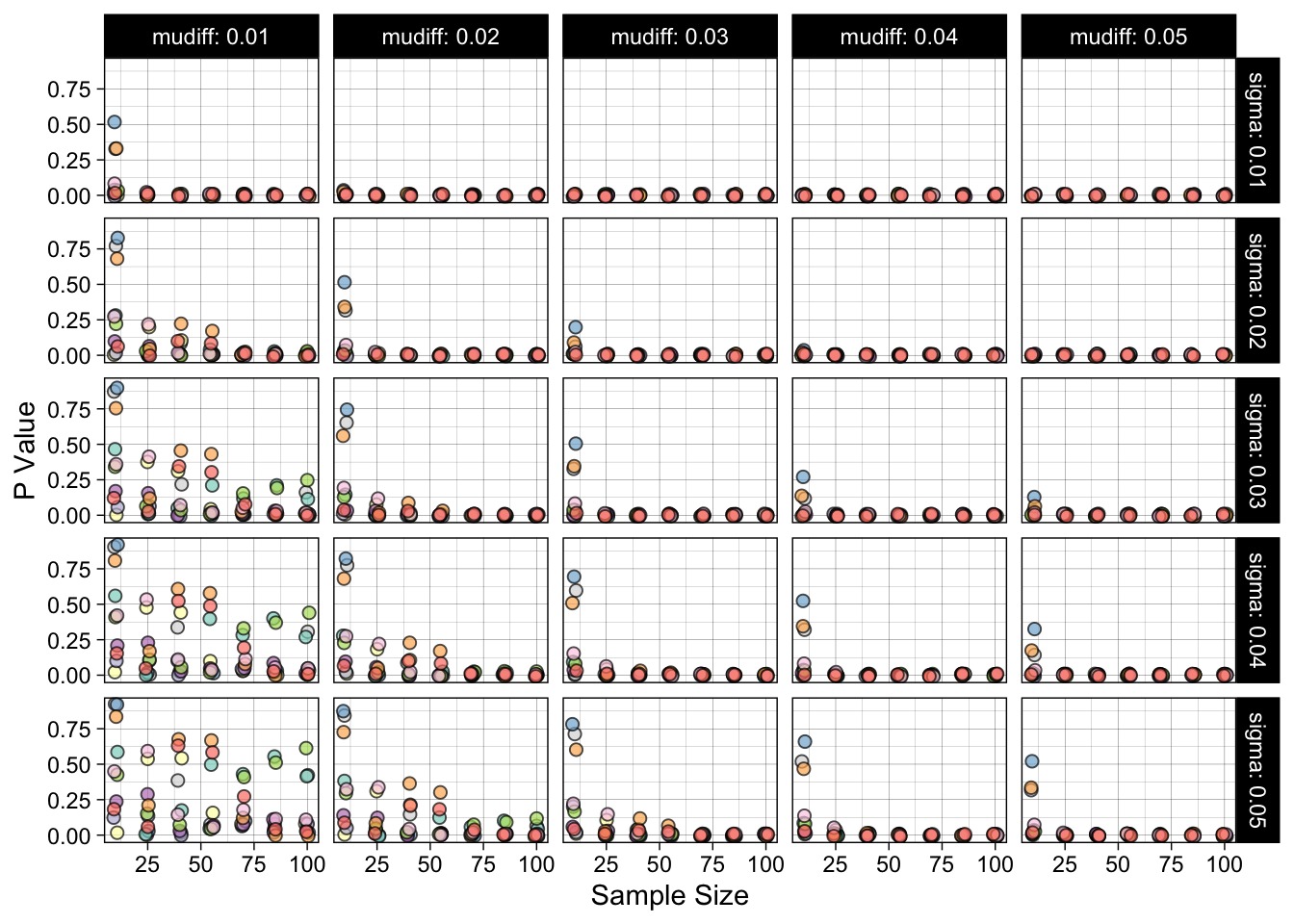
# 参数对P值稳定性的影响
df |>
ggplot(aes(nsize, p_value)) +
geom_jitter(
aes(fill = factor(seed)),
col = "black",
shape = 21,
width = 1,
height = 0.01,
alpha = .7,
size = 2
) +
scale_fill_brewer(palette = "Set3", guide = "none") +
facet_grid(sigma ~ mudiff, labeller = label_both) +
theme_linedraw() +
labs(x = "Sample Size", y = "P Value")